二、报告正文
1.研究计划要点及执行情况概述。 本研究的研究要点有如下两个方面:
1)从借款人的大量特征中,自动识别影响借款人产生不良借贷的主要因素, 并描述不良借贷用户的用户画像。本研究将借贷状态划分为良好和不良两类, 并对数据进行清洗,删除缺失率过高的数据、重复数据和无关特征后,对非数 值型数据进行哑变量编码,并对所有数据进行最大最小归一化的去量纲处理, 最后结合随机森林和梯度下降树模型,从数据集中150个数据特征中筛选出对 这两类状态的区分度最高的特征,作为影响借款人产生不良借贷的主要因素。 2)构建模型预测借款人的借贷状态,并分析其在预测借款人违约风险上与常用 经典模型的差异。本研究在研究1)的基础上,对良好借贷的用户样本进行了 下采样,在保证样本平衡的基础上,用随机森林、梯度下降树、多层感知机和 传统的逻辑回归模型构建借贷状态二分类模型,最后比较了其性能差异。 1.1研究背景
近年来,互联网与金融的结合更加广泛,互联网金融凭借其支付优势、流 程优势等优势逐渐深入人心,同时也对我国经济的发展起到了很大的促进作 用。其中,P2P网络借贷是互联网金融的一个分支。P2P(Peer to Peer)网络 借贷,通常是指个体和个体通过互联网平台进行的直接借贷活动。贷款发放的 决策过程被赋予到私人贷款人和借款人手中,P2P网贷平台上的借款人一般会 描述其贷款目的,并提供目前的财务状况如收入等,然后贷款人可根据这些信 息定位贷款的利率。对于借款人而言,P2P网贷是一种没有金融机构参与贷款 决策过程的贷款方式,也为比在传统银行系统获得更好的贷款条件提供了可 能。投资人也可把它看作是一种投资风险与贷款信用评级相联系的投资模式, P2P网贷平台本身通过提高成功交易的费用实现盈利的目的。
P2P网络借贷开始出现是在英国,因为其相较于传统银行更加方便,回报 率高,很快便快速蔓延至其他国家。艾瑞咨询统计结果显示,截至2017年, 我国网络借贷超过了 2万亿元,且年增长率高达40%,用户高达2亿人,相较 2016年增长23.1%,可见网络借贷发展之蓬勃。目前全球最大的P2P平台是成 立于美国的Lending Club。Lending Club 2014年在纽交所上市,是全球首家 上市的P2P平台。公司在运营初期仅提供个人贷款服务,至2012年平台贷款总 额达10亿美元规模。截至2015年年底,Lending Club共发放160亿美元贷 款,而他的另一大竞争对手P2P平台Prosper发放贷款总额仅为50亿美元。 即使国外的信用评估体系相当完备,信用风险仍然是P2P网贷平台的首要风 险。2016年上半年Lending Club爆出违规放贷丑闻,创始人离职,股价持续 下跌,全年亏损额达1.46亿美元。为降低借贷风险,Lending Club希望通过 有效的信用评估体系筛选优质借款人、保留一般借款人、拒绝风险较高借款 人,并根据不同信用等级划分,实现借款利率差异化定价。因此,Lending Club制定了严格、严谨、有效的信用评估系统,结合外部评分和内部评级,在 最大程度上规避坏账风险。总之,Lending Club作为业内最大的P2P平台,其 发展历史、信贷历史数据和对信用评估系统我国网贷行业发展有着重要的借鉴 意义。
相较于国外,我国的P2P行业市场尚不成熟。2007年6月,我国第一家 P2P网贷公司成立,从此网络借贷在我国拉开了序幕。在2013年前,我国 P2P网贷平台发展的很慢,属于萌芽期。2013年开始,我国P2P网贷行业在用 户和平台都开始爆发性增长。但是在爆发性增长的同时也伴随着很多风险,截 至2017年,停业的P2P网贷平台已达1500家,网贷平台坏账率普遍达到了 10%以上,这显著高于传统金融机构。网贷平台的高风险,有一个主要原因是, 网贷不需要抵押,借款人违约成本较低,如果出现很多借款人违约,则会对平 台现金流产生影响,会影响平台的可持续发展。在此背景下,对借款者的违约 风险进行分析显得尤为重要。
近些年来,越来越多的新业态金融公司利用数据挖掘(Data Mining)模型 预测借款人的违约概率。数据挖掘技术的应用势必会对传统金融业的信用评估 体系带来巨大冲击,为探索如何向传统金融未覆盖的大量中小微企业和普通个 人提供金融服务创造了新的路径和解决方式。相较于传统的信用风险评估模 型,数据挖掘模型主要有三点优势。第一,传统的信用风险评估模型大多使用 参数模型或者回归分析,有较严格的前提假设,比如OLS回归要求样本服从正 态分布、无噪声且序列不相关,Logistic模型要求解释变量之间相关性较小, 而数据挖掘模型的样本则基本没有相关限制。第二,数据挖掘模型可以利用更
多的信息,只要计算机的性能允许,可以不考虑特征选择的问题。第三,不同 的数据挖掘模型分别针对的问题有所差异,所以可以选择在不同情况下表现最 优的数据挖掘模型进行预测,相应准确率也更高。比如,神经网络(Neural Network, NN)模型和支持向量机(Support Vector Machine, SVM)模型适 合构建非线性函数;决策树(Decision Tree,DT)模型效率高,可以被转换为 易于理解的规则;随机森林(Random Forest, RF)和梯度下降树(Gradient Boosting Decision Tree, GBDT)等树模型可以处理高维度数据并给出不同特 征的重要性。
网络借贷与传统金融的风控体系有着本质差别。一方面,网络借贷主要是 依靠互联网技术和数据挖掘算法对借款人的信用风险进行评估和定价,不像传 统金融机构那样依赖于人工的审核和授信;另一方面,网络借贷的数据来源更 加多元化,能够对借款人进行更生动的肖像刻画。因此,本文以网络借贷为 例,利用Lending Club平台1455926个借款人2017年至2019年的数据,利用 树模型识别能够影响借款人发生不良借贷的主要因素,并利用数据挖掘模型构 建不良借贷预测模型,为违约风险的识别和预测提供了新的思路。
1.2文献综述
现有关于研究借款人违约风险问题的文献,基本上可以概括为两类:一类 是研究借款人违约的可能性(Probability of Default),另一类是研究借款人 违约的影响因素。前者关注借款人还款的结果,而后者更关注借款人还款决策 的过程。经典的预测借款人违约的模型包括Logistic、线性概率模型、Probit 等,但是预测效果受到的限制较多。一方面,样本的分布基本有严格要求,否 则,预测效果的偏误较大;另一方面,适配度(goodness of fit)的检验不 适用于存在非线性关系的样本。
相较于经典模型,数据挖掘模型则没有太多限制。虽然针对不同的样本, 不同类型的数据挖掘模型的预测效果也略有不同,但大多数时候的表现要优于 经典模型。并且,数据挖掘模型一直在开发中,特别地,随机森林模型是2001 年才提出的。所以,国内的文献中使用数据挖掘模型的文章并不算太多,而且 应用领域也较为分散。范超等对比了 SVM、树类模型等非线性模型与 Logistics、Probit等经典模型预测P2P平台出现问题的概率,发现SVM、树 类模型等非线性模型的预测效果更好。方匡南等利用某商业银行信用卡部的数 据库,对比了不同模型预测信用卡信用风险的效果,实证结果表明随机森林模 型要优于Logistic和SVM模型。吕劲松等将数据挖掘模型应用于商业银行信 贷资产质量审计之中,SVM模型有效地识别出了一部分被错误分类的贷款。
至于分析违约风险影响因素的文献,大致可以分为三个层面:一是宏观因 素,比如经济增长、利率等;二是行业因素,比如银行资本比率、内部管理 等;三是借款者个人因素,比如收入、还款记录等。由于信息不对称使得投资 人和网贷平台不能很好地评价借款人违约风险的大小,从而增加了投资者和网 贷平台的风险。借款人声誉能有效缓解信息不对称,声誉变量包括借款人以往 违约次数和借款成功次数为代表,实证得出借款人声誉对违约风险的识别效 应,且如果借款人还款能力增加,这种识别能力也会增强。以拍拍贷为例,研 究学历在网络借贷上的作用,发现随着学历的上升,借款人逾期的风险越小, 且借款成功的概率更高。另外,社会资本的存在能有效降低借款人的违约风 险,这些社会资本包括借款列表被推荐的额次数、是否加入小组、增加投资者 中朋友的个数等等。通过使用多元线性回归模型对拍拍贷进行违约风险分析, 发现随着年龄的增加违约风险越低。
然而,违约风险的影响因素选取大多具有一定的主观性,而且难以判断其 是否是影响被解释变量的关键变量。近些年,随机森林等树模型开始被用于选 取解释变量,因为其能根据解释变量在结果预测中的重要性进行排序,避免了 人为选取解释变量的主观性。方匡南和吴见彬使用随机森林模型选取了对被解 释变量影响程度最重要的前6、8、10个变量,分别对个人住房贷款违约进行 预测,发现随机森林的预测准确率明显高于其他模型。
纵观现有的文献,主要有以下两个方面值得进一步研究:第一,大多数文 献都集中于使用回归分析等经典方法预测违约风险,数据挖掘模型的使用较 少。数据挖掘模型相较于经典模型受到的限制条件较少,而且预测准确度也较 高,有广泛的应用空间。第二,大多数文献在违约风险影响因素的选取上大多 采用人为选取,分析方式依赖于对信贷业务的理解和作者自身的金融知识背 景。使用数据挖掘模型筛选变量则极大地减少了主观性和个体差异,筛选出的 特征也有助于进一步地构建违约风险预测模型。
1.3研究问题
基于现有研究和Lending Club 2017-2019年的借贷分析数据,该报告主要 研究以下两个问题:
1) 从借款人的大量特征中,自动识别影响借款人产生不良借贷的主要因 素,并描述不良借贷用户的用户画像。本研究拟将借贷状态划分为良好和不良 两类,使用随机森林和梯度下降树模型并基于数据集中所有有效的数据特征, 筛选对这两类状态的区分度最高的特征。
2) 构建模型预测借款人的借贷状态,并分析其在预测借款人违约风险上与 常用经典模型的差异。本研究将利用随机森林、梯度下降树、多层感知机和传 统的逻辑回归模型,构建借贷状态二分类模型,并比较其性能差异。
1. 4数据挖掘模型
数据挖掘模型根据所需目的不同,种类也非常多,本研究涉及的数据挖掘 模型主要是运用于分类和预测方面,共有四种,分别是随机森林(RF)、梯度下 降树(GBDT)、支持向量机(SVM)和神经网络(NN)。这四种模型都是有监督学 习算法,即通过训练样本获得最优模型,再利用最优模型预测测试样本的算 法。
1. 4. 1 Logistic 模型
在解决现实问题的过程中,经常需要研究某一事件发生的概率,以及哪些因 素以多大程度决定最终概率的大小。Logistic回归模型是一种广义线性模型, 其因变量服从二项分布,自变量的线性预测与因变量的Logit变换相关联。给 定一组客户样本T = {(&况)}无1,& e欧是客户的特征变量,必e (0,1}一个二分 类的属性变量,北=1表示第i个借款人的借款状态为不良,必=0表示良好,用 Logistic回归方法建立信用评分模型的目的是对指定的借款人评估其借款状态 不良的概率,Logistic回归方程表达式如式:
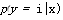 exp(6o + 阡 X)
exp(6o + 阡 X)
1 + exp(p0 + PTX)
其中p(y = 1|X)表示为不良借贷概率,X是m维向量,是m维待估计参数。
Logistic回归方程不能利用通常的最小二乘法来估计,而要用极大似然法来估计, 其原理可以简单描述如下:
假设总体*,的,…,塌由N个个体组成,每次从中抽取九个样本,其观测值记为
71,72,…,%。
给定&的条件下得到结果yt = 1的条件概率记为Pi = p(yi = 1\xi),则在同样 条件下得到结果必=0条件概率为汉必=0&) = 1-Pt。于是,该观察值的概率 为:
P(3)= Piyi(1-pi)1~yi
由于各项观察相互独立,因此可以得到其联合分布函数表达式:
n
郷0危1,■■■,%)=日卩产- Pi)1-yi
i=1
为了求出上式最大值,对等式两边取自然对数:
ln|X(KoM1,“"m)]
n
yi(Po + B1Xi1 + …+ Pm^im) -ln(1 + e髙邛网+…邛
i=1
上式称为似然对数函数。为了估计似然对数函数中的参数,对上式取最大值, 并分别对求偏导数,令其为0,得到:
 ePo+PixH+^+Pmxim
ePo+PixH+^+Pmxim
1 + eBo+BiXii Pmxim

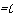 / qPo+P1xii+ Pmxim \
/ qPo+P1xii+ Pmxim \
),1 + ePo+P1xi1+^+Pmxim] &丿
1 = 1 ' /
j = 1,2, ...,m
上述方程称为似然方程。线性回归由于待估计的参数是线性的,可以通过偏 差平方和分别对参数求偏导数得到显式解;但由于Logistic回归中的似然方程 是非线性的原因,无法获得显示解,必须通过计算机程序迭代方式求解,在计算 机技术飞速发展的今天,迭代程序已经非常普遍,促进了 Logistic回归的应 用。
对似然方程提供的厨。=1,2 ...m)的估计值称为极大似然估计,而相应的条
件概率Pj的估计值(j = 1,2,…,m)是在给定&的条件下yt = 1的概率估计,它代
表了 Logistic回归模型的预测值或拟合值。
 当样本随机时,可以证明Logistic回归模型的极大似然估计具有有效性、一 致性以及渐进正态性等特点。容易得到如下等式:
当样本随机时,可以证明Logistic回归模型的极大似然估计具有有效性、一 致性以及渐进正态性等特点。容易得到如下等式:
=^0 + 81X1 + ^2%2 + + Pnxn
上式也称为Logistic线性回归模型,左边可以看作不良借贷发生比(Odds
to be bad)的对数,也称为概率p(y = 1\X)的Logit变换,即Logisitic概率单位
(Logistic Probability Unit),Logit值越高,该借款人发生不良借贷的概率越大,
违约的可能性也就越大。
此外,利用Logistic回归方法,可以对特征变量以及客户违约发生比之间的 关系进行定量研究和解释,例如可以估计某个特征变量取值的变化对违约概率的 影响大小,这一点对个人信用评分模型来说比较重要。在建模经验不足的时候, 哪些变量对客户的信用评级有决定性的影响,可以通过Logistic回归模型进行 初步探讨。
1.4.2决策树
决策树是随机森林和梯度下降树的基础。决策树是一种非线性判别分析方法, 是从机器学习领域中逐步发展出来的一种分类函数逼近方法,本质上是通过建立 一系列树形规则实现对样本分类的过程,即根据已知样本的属性和分类结果,生 成一系列树形分类器规则,利用这些规则对未知数据进行分类和预测,是一种典 型的有监督单分类器。决策树有三种类型的节点:根节点、叶子节点和中间节点, 每个节点都是一个对象的具体某个属性,从每个节点向下一层又可以分叉,生 成新的路径,该节点有多少属性集合,便有相应的分叉路径与之对应。这样, 从最上面的根节点出发,沿着某条路径,途径若干个中间节点,最后会到达某个 叶子节点,这条路径可以看作是一个分类的具体规则,而整个决策树就是由一系 列路径所构成的分类规则集合。从根节点出发,存在且只有一条路径能够到达最 终的叶子节点,保证决策树的输出是唯一的,决策树的结果可用于数据的分类和 预测。决策树的具体应用过程包含三个步骤:
第一步是对训练样本集进行分析,通过递归调用,生成倒立的树状拓扑结构; 第二步对生成的倒立树从根到叶子节点的各条路径进行分析,生成具体的分 类规则;
第三步是利用生成的分类规则,对新的数据进行分类预测,得到想要的结果。

图2-1决策树原理示意图
图2-1展现了决策树的基本原理,对于一个新的用户,如果用户的各项属性信 息为:“无房产”、“单身”、“年收入5.8万元”,通过上面构造的决策树, 从上图蓝色虚线路径的决策过程可以预测,该用户应该属于“无法偿还债务”。 此外,还可以得知“是否拥有房产”与“偿还债务”的关联性非常大。
决策树的实现算法一般有三种:ID3、C4.5和CART,本文所使用的是CART 算法。CART算法以递归的形式将n维空间划分割为不同区域。步骤分为两步:
(1) 选取一个属性爲,根据爲中的某个值将九维空间分为两个部分,一部分中 所有样本都满足,另一部分所有样本都满足;
(2) 按照第一步重新选择一个属性划分,不断递归直至九维空间都被划分。 属性划分的标准用的是Gini指标。假设数据集D有C种类别,那么数据集奶的Gini 不纯度指标可以定义为:
C
Gini(奶)= 1~^Pi
i=1
0表示类别i样本所占总样本的比例,当数据集中种类越多,Gini值越大,当 数据集只有一种类型,Gini值为0。
若所选取的属性为A,其所在的数据集D被分为k个奶子数据集。分裂后 数据集D的Gini为:
Gini^(D)= £黑g)
j=i
\D\代表数据集D的样本数,|奶|代表数据集奶的样本数。选择使得分裂后Gini 值最小的方案作为特征选取的标准。而结点分裂的条件则选取Gini增益值最大的 属性的类型作为判断条件。Gini增益值为:
AGini(A) = Gini(奶)—Gini』(D)
1.4.3随机森林
决策树模型虽然简单、运行速度快,但是易出现过度拟合(Overfitting)问 题。为了解决这个问题,一个自然的想法就是将单棵决策树组合为多棵决策树, 这些决策树在精度上没有显著要求,然后让所有的决策树以投票的形式对最终分 类结果进行表决,类似专家开会投票表决一样,在这个思想的启发下产生了随机 森林(Random Forest)模型。
随机森林模型是2001年由美国科学家Leo Breiman提出的一种机器学习 算法,以数据为驱动,通过对指定样本进行学习和训练得出分类规则,不需要任 何分类的先验知识,是一种非参数分类模型。随机森林可以看作是一种集成学习 模型,基本分类器由决策树组成,这些决策树是经过Bagging集成学习技术得 到,对单棵决策树的输出结果进行投票从而决定随机森林模型最终的分类结果。 随机森林对噪声和异常值有着很好的过滤效果,能够克服过拟合问题,尤其在对 高维数据的分类方面表现除了良好的并行性和可扩展性。图2-2描述了随机森林 的基本原理。
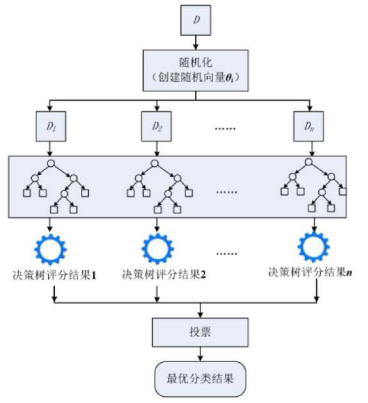
图2-2随机森林的基本原理
随机森林的算法实现可以描述为:假设有一个样本集9,从中有放回地随机 生成同分布的向量序列= 1.. k),同时有放回地随机抽取特征序列Xi(i = 1..k),由&和饥生成CART的决策树心缶),多个决策树构成了随机森林 {h(xk,ek),k = 1..m},根据决策树的输出结果进行投票,得票最多的分类结果就 是最优分类方式。
给定一组随机森林hi(X),h2(X),…,hk(X),从随机向量{匕X}中得到训练集, 边际方程(Marginal Function )定义如下:
mg(X, Y) = avkI(hk(X) = Y) - maxj^YavkI(hk(X) = j)
【(•)是指示函数(Indicator Function),边际函数测度的是平均分类正确的数 量超过平均分类错误的数量的程度,边际函数值越大,分类预测的可信度越高。 一般误差可以写成:
PE* = Px:Y(mg(X,Y)<0)
当决策树的数量不断增加,对于几乎绝大多数序列6i,^,PE*都收敛如下: Px,Y(Pe(h(X,d) = Y)- maxj^kPe(h(X,e) = j) < 0)
所以,随机森林并不会因为决策树增加而导致过度拟合的问题。同时,随机 森林还可以计算每个特征的重要性程度,基本的思想是对已有的随机森林,用袋 外数据(Out of Bag,OOB)测试其准确率;然后改变其中某个特征的值,即加 入噪声干扰,再计算已有随机森林新的袋外数据准确率;那么,该特征的重要性 程度就是原始袋外数据的准确率减去加入干扰后袋外数据的准确率。
1.4.4梯度下降树
GBDT全称Gradient Boosting梯度提升树,是一种基于Boosting提升树的 算法。Boosting思想是构建很多棵回归树(回归决策树),开始时每个样本权重一 样,用第一棵树来学习模型,后一棵树降低上一颗棵学习好的样本权重,增大没 有学习好的样本权重,即重点学习上一棵树的残差(预测值与真实值的差)最后 将这些回归树线性加权。而GBDT就是在Boosting上加入了梯度下降算法,每一 次建立回归树是在之前建立回归树损失函数的梯度下降方向,使得残差往梯度方 向上减少,速度更快。GBDT的算法流程如下:假设我们前一轮迭代得到的回归 树是/t_i(%),损失函数是:
L(y,/t_i(x))
式中%为输入值,y为真实值,/t_i(x)为模型预测函数。计算损失函数的负梯 度为:
3L(yi,f(xi)')
之后得到本轮损失函数:
L(y,ft(x)) = L(y,ft_1(x) + ht(x))
则式中ht(x)为本轮需要寻找的弱回归树。针对每一个叶子节点里的样本,我 们求出使损失函数最小,也就是拟合叶子节点最好的的输出值ctj:
n
勺=argmin 2 ▲⑴,左_1(&) + C)
1=1
式中,c为拟合叶子节点索引。之后得到了本轮的决策树拟合函数如下:
t
ht(x) = 2 W
j=i
式中I为单位矩阵。最后,本轮最终得到的强回归树的表达式如下:
t
ft(x) = ft_i(x) + 2ctjI
j=1
1.4.5神经网络
神经网络模型是模拟生物神经网络的算法,其涉及的具体算法有很多种,本 文使用的是多层感知机(Multi-layer Perceptron,MLP)算法。MLP是一种特殊 的有向图,结点被看作神经元,连接结点的有向弧被看作连接神经元的神经。 MLP的结构一般分为三个部分:输入层、隐藏层和输出层,如图2-3所示:

图2-3多层感知机原理示意图
神经元之间的传导需要用一个激活函数进行分类(激活为1,未激活为0), 常见的激活函数有sigmod或者tanh,当该神经元超过一定阈值时,此神经元 被激活传导到下一神经元。输出层则极小化以下的损失函数:
|
O = 一{} [zlog(y~) + (1 - z)log(l - y)]} (*) |
其中, 的概率。 |
X为输入特征;Z为输入特征对应的激活值,取值为0或1; y为z对应 |
2.研究工作主要进展及所取得的研究成果。
2.1数据分析和模型实现
本研究的数据来源是Lending Club信贷平台上2017年至2019年共1455926 个借款人的借贷数据,每个借贷人有153项数据特征,包括申请贷款金额、贷款 目的、年收入等个人信息,也包括发放金额、利率、用户评级等表示借贷人在 Lending Club借贷状态的信息。
本研究的主要任务是:
1) 结合梯度下降树和随机森林模型,从153项特征中筛选出区分不良借贷 的主要影响因素。
2) 根据计算得到的主要影响因素,分别描述Lending Club的贷款发放特征 以及良好借贷和不良借贷的借款人区别。
3) 根据随机森林、梯度下降树、多层感知机模型和Logistic模型,构建不良 借贷状态的分类预测模型。
2.2特征筛选
2.2.1借贷状态
首先观察目标变量一一借贷状态的数据分布情况。借款人的借贷情况分为七
类:正常还款、已还完、注销、在宽限期、拖欠16-30天、拖欠31-120天、违约。 该报告设定拖欠16-30天、拖欠31-120天、违约为不良借贷状态,其他状态为良好 借贷状态。图2-1(左)是借款人借贷状态的分布情况。图2-1(右)是2017-2019 年每季度的借贷状态数量变化。